#1 · 12.10.2019, 16:03

Цитата: Удаленный пользователь от 12.10.2019, 16:03
Гипотеза Коллатца

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

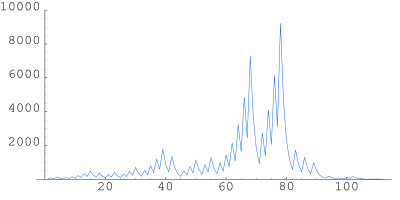
График последовательности для числа 27

Гипо́теза Коллатца (3n+1 дилемма, сираку́зская пробле́ма) — одна из нерешённых проблем математики. Получила широкую известность благодаря простоте формулировки. Названа по имени немецкого математика Лотара Коллатца (англ.), сформулировавшего эту задачу 1 июля 1932 года.^[1]

Формулировка

Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.

Гипотеза Коллатца заключается в том, что какое бы начальное число n мы ни взяли, рано или поздно мы получим единицу^[2].

Примеры

Например, для числа 3 получаем:

3 — нечётное, 3×3 + 1 = 10

10 — чётное, 10:2 = 5

5 — нечётное, 5×3 + 1 = 16

16 — чётное, 16:2 = 8

8 — чётное, 8:2 = 4

4 — чётное, 4:2 = 2

2 — чётное, 2:2 = 1

1 — нечётное, 1×3 + 1 = 4

Очевидно, что, начиная с 1, начинают циклически повторяться числа 1, 4, 2.

Последовательность, начинающаяся числом 19, приходит к единице уже за двадцать шагов:

19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, …

Для числа 27 получаем:

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, …

Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232.

Чи́сла-гра́дины — также распространённое название для совокупности рассмотренных последовательностей. Такое название возникло из-за того, что графики последовательностей (см. иллюстрацию) похожи на траектории движения градин в атмосфере.

Проект «Collatz Conjecture»

В августе 2009 года на платформе BOINC был запущен проект добровольных распределённых вычислений «Collatz Conjecture»^[3], целью которого является проверка гипотезы Коллатца на больших числах. Вычислительный модуль проекта может использовать вычислительные мощности современных видеокарт.

Кроме проекта Collatz Conjecture, с августа 2017 года поиском решения этой проблемы стал также заниматься и проект распределённых вычислений yoyo@Home http://www.rechenkraft.net/yoyo/

По состоянию на апрель 2019 года проверены все натуральные числа меньше чем 1 152 921 504 606 846 976 и каждое из них за конечное количество шагов соответствовало условиям Гипотезы Коллатца.

См. также

Открытые математические проблемы

BOINC

Гипотеза Коллатца

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

График последовательности для числа 27

Гипо́теза Коллатца (3n+1 дилемма, сираку́зская пробле́ма) — одна из нерешённых проблем математики. Получила широкую известность благодаря простоте формулировки. Названа по имени немецкого математика Лотара Коллатца (англ.), сформулировавшего эту задачу 1 июля 1932 года.^[1]

Формулировка

Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.

Гипотеза Коллатца заключается в том, что какое бы начальное число n мы ни взяли, рано или поздно мы получим единицу^[2].

Примеры

Например, для числа 3 получаем:

3 — нечётное, 3×3 + 1 = 10

10 — чётное, 10:2 = 5

5 — нечётное, 5×3 + 1 = 16

16 — чётное, 16:2 = 8

8 — чётное, 8:2 = 4

4 — чётное, 4:2 = 2

2 — чётное, 2:2 = 1

1 — нечётное, 1×3 + 1 = 4

Очевидно, что, начиная с 1, начинают циклически повторяться числа 1, 4, 2.

Последовательность, начинающаяся числом 19, приходит к единице уже за двадцать шагов:

19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, …

Для числа 27 получаем:

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1, …

Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232.

Чи́сла-гра́дины — также распространённое название для совокупности рассмотренных последовательностей. Такое название возникло из-за того, что графики последовательностей (см. иллюстрацию) похожи на траектории движения градин в атмосфере.

Проект «Collatz Conjecture»

В августе 2009 года на платформе BOINC был запущен проект добровольных распределённых вычислений «Collatz Conjecture»^[3], целью которого является проверка гипотезы Коллатца на больших числах. Вычислительный модуль проекта может использовать вычислительные мощности современных видеокарт.

Кроме проекта Collatz Conjecture, с августа 2017 года поиском решения этой проблемы стал также заниматься и проект распределённых вычислений yoyo@Home http://www.rechenkraft.net/yoyo/

По состоянию на апрель 2019 года проверены все натуральные числа меньше чем 1 152 921 504 606 846 976 и каждое из них за конечное количество шагов соответствовало условиям Гипотезы Коллатца.

См. также

hoarfrost и atch отреагировали на эту запись.

#2 · 18.11.2019, 10:24

У всех все нормально с расчетом этого проекта? Что-то у меня со вчерашнего дня задания начали пачками валиться в ошибку.

#3 · 06.08.2021, 13:37

На днях появилось интересное видео о гипотезе Коллатца

hoarfrost, PinkFloyd и Pavel Kirpichenko отреагировали на эту запись.

#4 · 06.08.2021, 17:34

Цитата: prb от 06.08.2021, 13:37

На днях появилось интересное видео о гипотезе Коллатца

https://www.youtube.com/watch?v=QgzBDZwanWA

Интересно. Даже посчитать проект захотелось.

prb отреагировал на эту запись.

#5 · 07.08.2021, 18:41

Видео действительно интересное. Математическая задача также интересна. Но сейчас, в период резкой нехватки добровольных вычислительных ресурсов, считаю наоборот, надо призывать усиливать медико-биологические проекты и те проекты, которые конечны, в первую очередь - это TN-Grid, Sidock@Home и Gerasim@Home

#6 · 08.08.2021, 19:19

Так Collatz Conjecture считают, в основном, на GPU.

#7 · 08.08.2021, 23:03

Yura12

Если Вы готовы доказать, что этот проект бесконечен, значит с легкостью докажете и гипотезу Коллатца.

Евгений и Шмяка отреагировали на эту запись.

#8 · 13.06.2022, 19:20

Цитата: Удаленный пользователь от 13.06.2022, 19:20
Дичь какая то происходит с Боинком последнее время, вот и этот проект отвалился: Завершите свою работу (thesonntags.com)

На этой неделе я потеряю свой «компьютерный зал» в подвале, пока будет сделано смягчение просачивания воды. После этого дом выходит на рынок, так как я буду переезжать в штат с более приятным климатом с меньшим количеством коррумпированных политиков и более низкими налогами. В результате проект Collatz будет закрыт в течение некоторого времени. Пожалуйста, настройте свои машины так, чтобы они не получали новой работы, потому что вы, вероятно, не сможете вернуть работу до истечения срока ее ожидания. Работа начинается в среду, поэтому я должен очистить все до этого, так что это может быть понедельник или вторник, когда он будет закрыт. Как только я перееду, я не знаю, насколько надежным будет широкополосный доступ, но я надеюсь, что, поскольку он будет основан на оптоволоконном, а не на кабельном телевидении, он будет приличным. Это должно быть быстрее и дешевле, но я не могу предсказать, когда проект Collatz вернется в онлайн в это время.

Дичь какая то происходит с Боинком последнее время, вот и этот проект отвалился: Завершите свою работу (thesonntags.com)

На этой неделе я потеряю свой «компьютерный зал» в подвале, пока будет сделано смягчение просачивания воды. После этого дом выходит на рынок, так как я буду переезжать в штат с более приятным климатом с меньшим количеством коррумпированных политиков и более низкими налогами. В результате проект Collatz будет закрыт в течение некоторого времени. Пожалуйста, настройте свои машины так, чтобы они не получали новой работы, потому что вы, вероятно, не сможете вернуть работу до истечения срока ее ожидания. Работа начинается в среду, поэтому я должен очистить все до этого, так что это может быть понедельник или вторник, когда он будет закрыт. Как только я перееду, я не знаю, насколько надежным будет широкополосный доступ, но я надеюсь, что, поскольку он будет основан на оптоволоконном, а не на кабельном телевидении, он будет приличным. Это должно быть быстрее и дешевле, но я не могу предсказать, когда проект Collatz вернется в онлайн в это время.